Konjungsi dan Disjungsi
Pernyataan
Kalimat yang mempunyai nilai kebenaran (benar atau salah, tetapi tidak kedua-duanya) disebut pernyataan
Contoh yang bukan kalimat pernyataan:
- Apakah kamu sudah makan? (Kalimat tanya)
- Minggir! (Kalimat perintah)
- Semoga panjang umur (Kalimat yang berisi harapan)
Pernyataan belum tentu bermakna. Contoh:
- Satu tambah satu sama dengan 2
- 3 adalah bilangan genap
- Roti adalah bilangan desimal
- Jeruk minum jeruk
Kalimat 1 dan 2 merupakan kalimat yang memiliki makna atau bisa disebut sebagai proposisi, sedangkan kalimat 3 dan 4 tidak memiliki makna sehingga tidak bisa dinyatakan kebenarannya.
flowchart LR
id1([Kalimat]) --> id2([Pernyataan/ Preposisi])
id1([Kalimat]) --> id3([Bukan Pernyataan])
id2([Pernyataan/ Preposisi]) --> id4([Benar])
id2([Pernyataan/ Preposisi]) --> id5([Salah])
Pernyataan Majemuk
Pernyataan majemuk dihubungkan dengan kata-kata perangkai
| Kata Penghubung | Lambang | Nama |
|---|---|---|
| dan | $\wedge$ | Konjungsi |
| atau | $\vee$ | Disjungsi |
| jika-maka | $\Rightarrow$ | Implikasi |
| jika dan hanya jika | $\Leftrightarrow$ | Biimplikasi |
Negasi (kebalikan) Berikut tabel nilai kebenaran negasi dari pernyataan $a$
$a$ $\neg a$ $\neg (\neg a)$ B S B S B S Contoh: Misalkan $a$ menyatakan “Air itu berwarna biru”, maka negasi $a$, yaitu $\neg a$ menyatakan “Air itu tidak berwarna biru” atau “Tidak benar bahwa air itu berwarna biru”.
Konjungsi Berikut tabel nilai kebenaran konjungsi dari pernyataan $a$ dan $b$
$a$ $b$ $a \wedge b$ B B B B S S S B S S S S Contoh:
Misalkan $a$ menyatakan “2 merupakan bilangan prima” dan $b$ menyatakan “2 merupakan bilangan genap”, $a \wedge b$ menyatakan bahwa “2 merupakan bilangan prima dan bilangan genap”. Apabila terdapat negasi pada $a$, sehingga menyatakan bahwa “2 bukan merupakan bilangan prima dan 2 merupakan bilangan genap”, pernyataan tersebut bernilai salah.
Disjungsi Berikut tabel nilai kebenaran disjungsi dari pernyataan $a$ dan $b$
$a$ $b$ $a \vee b$ B B B B S B S B B S S S Contoh:
Misalkan $a$ menyatakan “$x=-1$ merupakan solusi dari $x^2+3x+2=0$ “ dan $b$ menyatakan “$x=2$ merupakan solusi dari $x^2+3x+2=0$ “, maka $a \vee b$ menyatakan “$x=-1$ atau $x=-2$ merupakan solusi dari $x^2+3x+2=0$ “. Apabila terdapat negasi pada $a$, akan menyatakan bahwa “x\neq -1” atau $x=-2$ merupakan solusi dari $x^2+3x+2=0$”, pernyataan tersebut bernilai benar.
Implikasi Berikut tabel nilai kebenaran implikasi dari pernyataan $a$ dan $b$
$a$ $b$ $a \Rightarrow b$ B B B B S S S B B S S B Contoh:
Misalkan $a$ menyatakan “$x$ merupakan bilangan genap” dan $b$ menyatakan “$x$ merupakan bilangan real” maka $a \Rightarrow b$ menyatakan “Jika $x$ merupakan bilangan genap, maka $x$ merupakan bilangan real”. Apabila terdapat negasi dari $a$, maka akan menyatakan “Jika $x$ merupakan bilangan genap, maka $x$ bukan merupakan bilangan real”, lawan dari bilangan real adalah bilangan imajiner, tidak mungkin bilangan genap adalah bilangan imajiner, sehingga pernyataan tersebut bernilai salah.
Biimplikasi
$a$ $b$ $a \Leftrightarrow b$ B B B B S S S B S S S B Contoh:
Misalkan $a$ menyatakan “x=17” dan $b$ menyatakan “$x^3$=4.913”, maka $a \Leftrightarrow b$ menyatakan “x=17 jika dan hanya jika $x^3=4.913$”. Apabila terdapat negasi pada $a$, akan menyatakan bahwa “$\neg$17 jika dan hanya jika $x^3=4.913$”, pernyataan bernilai salah.
Konvers, Invers, dan Kontraposisi
| $a$ | $b$ | $a\Rightarrow b$ | $b\Rightarrow a$ | $\neg a \Rightarrow \neg b$ | $\neg b \Rightarrow \neg a$ |
|---|---|---|---|---|---|
| B | B | B | B | B | B |
| B | S | S | B | B | S |
| S | B | B | S | S | B |
| S | S | B | B | B | B |
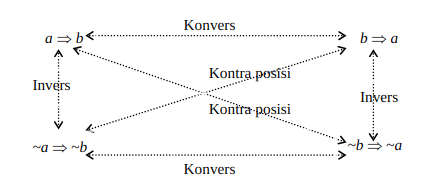
Apabila diketahui $a \Rightarrow b$, maka
- Konvers dari $a \Rightarrow b$ adalah $b \Rightarrow a$
- Invers dari $a \Rightarrow b$ adalah $\neg a \Rightarrow \neg b$
- Kontraposisi dari $a \Rightarrow b$ adalah $\neg b \Rightarrow \neg a$
Argumen
Tautologi
Tautologi adalah pernyataan majemuk yang selalu benar, contoh: $a$ = Jono makan roti $\neg a$ = Jono tidak makan roti Kalimat majemuk $a \vee \neg a$ akan selalu bernilai benar.
Argumen Interferensi
- Modus Ponens [MP] $p \Rightarrow q, p \models q$
- Modus Tolens [MT] $p \Rightarrow q, \neg q \models \neg p $
- Constructive Dilemma [CD] $(p \Rightarrow q) \wedge (r \Rightarrow s), p \vee r \models (q\vee s)$
- Disjunctive Syllogism [DS] $p \vee q, \neg p \models q$
- Hypothetical Syllogism [HS] $p \Rightarrow q, q \Rightarrow r \models p \Rightarrow r$
- Conjunction [Con] $p,q \models p \wedge q$
- Simplification [Sim] $p \wedge q \models p$
- Addition [Add] $p \models p \vee q $
Aturan Penggantian
Asosiatif [Aso]
\[\begin{array}{rcl} p\wedge q \wedge r &\Leftrightarrow &p \wedge (q \wedge r)\\ p\vee q \vee r &\Leftrightarrow &p \vee (q \vee r) \end{array}\]Komulatif [Kom]
\[\begin{array}{rcl} p\wedge q &\Leftrightarrow &q \wedge p\\ p\vee q &\Leftrightarrow &q \vee p \end{array}\]Distributif [Dis]
\[\begin{array}{rcl} p\wedge (q\vee r) &\Leftrightarrow &p \wedge q \vee p \wedge r \\ p\vee q \wedge r &\Leftrightarrow &(p \vee q) \wedge (p \vee r) \end{array}\]Kontraposisi [Kon]
\[p\Rightarrow q \Leftrightarrow \neg q \Rightarrow \neg p\]Negasi Ganda [NG]
\[p \Leftrightarrow \neg \neg p\]De Morgan [DM]
\[\neg(p \wedge q) \Leftrightarrow \neg p \vee \neg q\]Idempoten [Ide]
\[\begin{array}{rcl} p \wedge p &\Leftrightarrow &p\\ p \vee p &\Leftrightarrow &p \end{array}\]Ekuivalensi [Eku]
\[\begin{array}{rcl} p \Leftrightarrow q &\Leftrightarrow & (p \Rightarrow q) \wedge (q \Rightarrow p)\\ p \Leftrightarrow q &\Leftrightarrow & p \wedge q \vee \neg p \wedge \neg q \end{array}\]Implikasi [Imp]
\[p \Rightarrow q \Leftrightarrow \neg p \vee q\]Eksportasi [Eks]
\[p \wedge q \Rightarrow r \Leftrightarrow p \Rightarrow (q \Rightarrow r)\]
Konsistensi Premis
Sumber
Drs. Sukirman, Logika Matematika